how to find hill coefficient from graph
The tutorial explains the nuts of correlation in Excel, shows how to summate a correlation coefficient, build a correlation matrix and interpret the results.
One of the simplest statistical calculations that you can practice in Excel is correlation. Though unproblematic, it is very useful in understanding the relations betwixt 2 or more variables. Microsoft Excel provides all the necessary tools to run correlation analysis, you just demand to know how to use them.
Correlation in Excel - the basics
Correlation is a mensurate that describes the strength and direction of a relationship betwixt two variables. Information technology is commonly used in statistics, economics and social sciences for budgets, business plans and the like.
The method used to report how closely the variables are related is called correlation analysis.
Here are a couple of examples of potent correlation:
- The number of calories you eat and your weight (positive correlation)
- The temperature outside and your heating bills (negative correlation)
And here the examples of data that have weak or no correlation:
- Your cat's name and their favorite food
- The color of your eyes and your height
An essential affair to understand near correlation is that it only shows how closely related two variables are. Correlation, yet, does not imply causation. The fact that changes in ane variable are associated with changes in the other variable does not mean that one variable really causes the other to modify.
If you're interested to learn causality and make predictions, take a pace forrad and perform linear regression analysis.
Correlation coefficient in Excel - interpretation of correlation
The numerical measure of the degree of clan between two continuous variables is called the correlation coefficient (r).
The coefficient value is always between -1 and ane and information technology measures both the strength and direction of the linear human relationship betwixt the variables.
Strength
The larger the absolute value of the coefficient, the stronger the human relationship:
- The extreme values of -1 and 1 indicate a perfect linear relationship when all the data points autumn on a line. In practice, a perfect correlation, either positive or negative, is rarely observed.
- A coefficient of 0 indicates no linear relationship between the variables. This is what you are probable to become with ii sets of random numbers.
- Values between 0 and +1/-i represent a scale of weak, moderate and stiff relationships. As r gets closer to either -1 or ane, the strength of the relationship increases.
Direction
The coefficient sign (plus or minus) indicates the direction of the relationship.
- Positive coefficients correspond direct correlation and produce an upward slope on a graph - as i variable increases and then does the other, and vice versa.
- Negative coefficients represent changed correlation and produce a downwardly slope on a graph - as one variable increases, the other variable tends to decrease.
For better understanding, please take a look at the following correlation graphs:
- A coefficient of 1 ways a perfect positive relationship - as one variable increases, the other increases proportionally.
- A coefficient of -i ways a perfect negative relationship - as one variable increases, the other decreases proportionally.
- A coefficient of 0 means no relationship between two variables - the data points are scattered all over the graph.
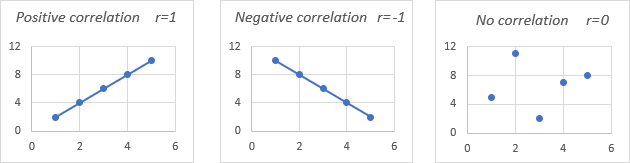
Pearson correlation
In statistics, they measure several types of correlation depending on blazon of the data you are working with. In this tutorial, nosotros will focus on the nigh common i.
Pearson Correlation, the total proper name is the Pearson Product Moment Correlation (PPMC), is used to evaluate linear relationships between information when a change in one variable is associated with a proportional change in the other variable. In uncomplicated terms, the Pearson Correlation answers the question: Can the data be represented on a line?
In statistics, it is the most popular correlation type, and if y'all are dealing with a "correlation coefficient" without farther qualification, it's most likely to be the Pearson.
Hither's the most commonly used formula to detect the Pearson correlation coefficient, also chosen Pearson's R:
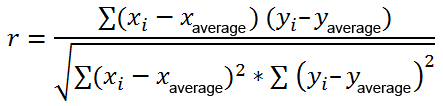
At times, you may come up across two other formulas for calculating the sample correlation coefficient (r) and the population correlation coefficient (ρ).
How to practice Pearson correlation in Excel
Calculating the Pearson correlation coefficient by mitt involves quite a lot of math. Luckily, Microsoft Excel has made things very uncomplicated. Depending on your information ready and your goal, you are free to apply i of the post-obit techniques:
- Find the Pearson correlation coefficient with the CORREL function.
- Make a correlation matrix by performing Data Analysis.
- Find multiple correlation coefficients with a formula.
- Plot a correlation graph to get the visual representation of the data human relationship.
How to calculate correlation coefficient in Excel
To compute a correlation coefficient past hand, you'd have to use this lengthy formula. To detect correlation coefficient in Excel, leverage the CORREL or PEARSON office and become the upshot in a fraction of a second.
Excel CORREL function
The CORREL function returns the Pearson correlation coefficient for two sets of values. Its syntax is very easy and straightforward:
CORREL(array1, array2)
Where:
- Array1 is the start range of values.
- Array2 is the second range of values.
The ii arrays should have equal length.
Assuming we have a set of independent variables (x) in B2:B13 and dependent variables (y) in C2:C13, our correlation coefficient formula goes as follows:
=CORREL(B2:B13, C2:C13)
Or, we could swap the ranges and still get the same result:
=CORREL(C2:C13, B2:B13)
Either way, the formula shows a strong negative correlation (near -0.97) between the boilerplate monthly temperature and the number of heaters sold:
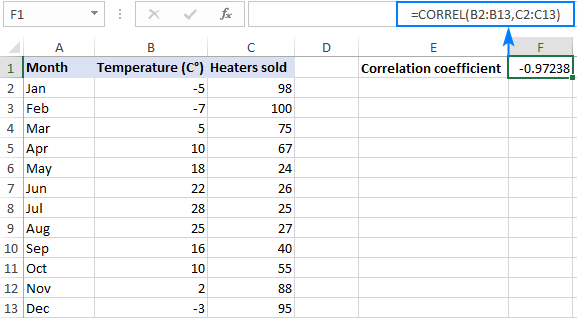
three things you should know nearly the CORREL function in Excel
To calculate the correlation coefficient in Excel successfully, please keep in listen these 3 simple facts:
- If ane or more cells in an array contains text, logical values or blanks, such cells are ignored; cells with zero values are calculated.
- If the supplied arrays are of different lengths, an #N/A error is returned.
- If either of the arrays is empty or if the standard divergence of their values equals zero, a #DIV/0! error occurs.
Excel PEARSON office
The PEARSON part in Excel does the same matter - calculates the Pearson Product Moment Correlation coefficient.
PEARSON(array1, array2)
Where:
- Array1 is a range of independent values.
- Array2 is a range of dependent values.
Because PEARSON and CORREL both compute the Pearson linear correlation coefficient, their results should agree, and they generally do in contempo versions of Excel 2007 through Excel 2019.
In Excel 2003 and earlier versions, however, the PEARSON function may display some rounding errors. Therefore, in older versions, it is recommended to use CORREL in preference to PEARSON.
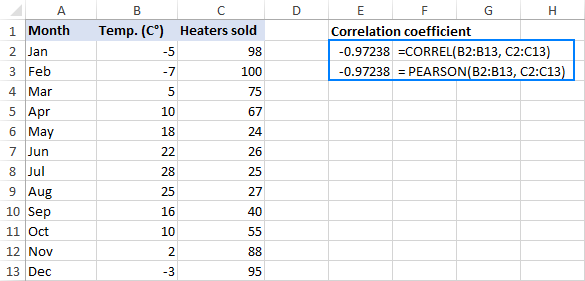
On our sample data set, both functions exhibit the same results:
=CORREL(B2:B13, C2:C13)
=PEARSON(B2:B13, C2:C13)
How to make a correlation matrix in Excel with Information Analysis
When yous demand to examination interrelations between more than 2 variables, information technology makes sense to construct a correlation matrix, which is sometimes chosen multiple correlation coefficient.
The correlation matrix is a table that shows the correlation coefficients between the variables at the intersection of the corresponding rows and columns.
The correlation matrix in Excel is built using the Correlation tool from the Analysis ToolPak add-in. This add-in is available in all versions of Excel 2003 through Excel 2019, but is not enabled by default. If y'all have not activated it yet, please exercise this now by post-obit the steps described in How to enable Data Analysis ToolPak in Excel.
With the Data Assay tools added to your Excel ribbon, you lot are prepared to run correlation analysis:
- On the top right corner of the Information tab > Analysis group, click the Data Analysis push.
- In the Information Assay dialog box, select Correlation and click OK.
- In the Correlation box, configure the parameters in this way:
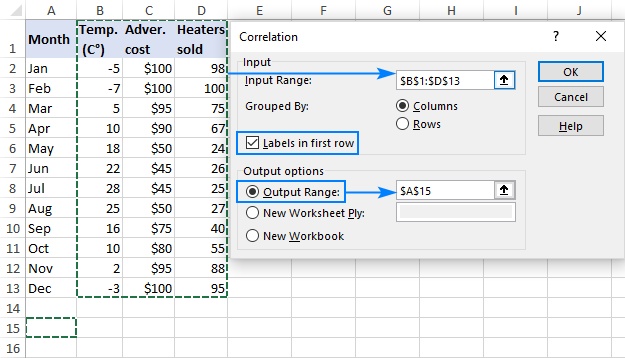
- Click in the Input Range box and select the range with your source information, including column headers (B1:D13 in our case).
- In the Grouped by section, brand certain the Columns radio box is selected (given that your source data are grouped into columns).
- Select the Labels in outset row check box if the selected range contains cavalcade headers.
- Choose the desired output option. To accept the matrix in the same sail, select Output Range and specify the reference to the leftmost cell into which the matrix is to exist output (A15 in this instance).
When done, click the OK button:
Your matrix of correlation coefficients is done and should wait something like shown in the next section.
Interpreting correlation analysis results
In your Excel correlation matrix, you can discover the coefficients at the intersection of rows and columns. If the column and row coordinates are the aforementioned, the value 1 is output.
In the in a higher place example, we are interested to know the correlation betwixt the dependent variable (number of heaters sold) and two independent variables (boilerplate monthly temperature and advertising costs). And so, nosotros look only at the numbers at the intersection of these rows and columns, which are highlighted in the screenshot below:
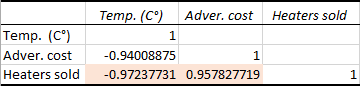
The negative coefficient of -0.97 (rounded to 2 decimal places) shows a potent inverse correlation between the monthly temperature and heater sales - equally the temperature grows higher, fewer heaters are sold.
The positive coefficient of 0.97 (rounded to 2 decimal places) indicates a stiff straight connexion betwixt the advertisement upkeep and sales - the more than coin you spend on advertising, the college the sales.
How to practise multiple correlation analysis in Excel with formulas
Building the correlation table with the Data Assay tool is easy. However, that matrix is static, meaning you will need to run correlation analysis anew every time the source information change.
The expert news is that you can hands build a like correlation table yourself, and that matrix will update automatically with each change in the source values.
To take it washed, use this generic formula:
CORREL(Kickoff(first_variable_range , 0, ROWS($1:ane)-1), OFFSET(first_variable_range, 0, COLUMNS($A:A)-one))
Important note! For the formula to work, y'all should lock the get-go variable range past using absolute cell references.
In our example, the first variable range is $B$2:$B$xiii (please notice the $ sign that locks the reference), and our correlation formula takes this shape:
=CORREL(OFFSET($B$2:$B$13, 0, ROWS($1:1)-1), OFFSET($B$two:$B$13, 0, COLUMNS($A:A)-1))
With the formula ready, allow's construct a correlation matrix:
- In the offset row and first column of the matrix, blazon the variables' labels in the aforementioned club as they announced in your source tabular array (please see the screenshot below).
- Input the above formula in the leftmost cell (B16 in our example).
- Drag the formula downward and to the correct to copy it to as many rows and columns as needed (3 rows and three columns in our instance).
As the result, we've got the following matrix with multiple correlation coefficients. Delight notice that the coefficients returned by our formula are exactly the aforementioned as output by Excel in the previous example (the relevant ones are highlighted):
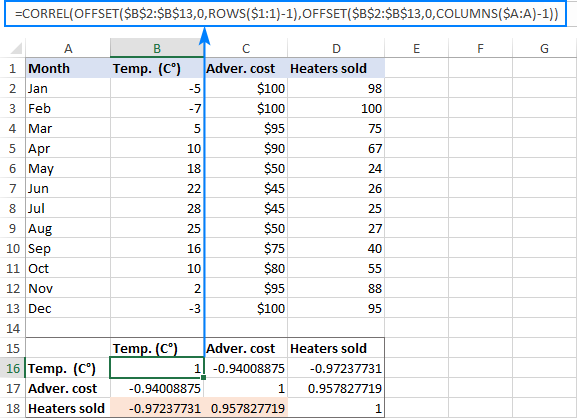
How this formula works
As yous already know, the Excel CORREL role returns the correlation coefficient for two sets of variables that you lot specify. The main challenge is to supply the appropriate ranges in the corresponding cells of the matrix. For this, you enter simply the starting time variable range in the formula and employ the following functions to make the necessary adjustments:
- Showtime - returns a range that is a given number of rows and columns from a specified range.
- ROWS and COLUMNS - return the number of rows and columns in a range, respectively. In our correlation formula, both are used with one purpose - get the number of columns to offset from the starting range. And this is achieved by cleverly using absolute and relative references.
To better understand the logic, let's see how the formula calculates the coefficients highlighted in the screenshot higher up.
First, let'southward examine the formula in B18, which finds correlation between the monthly temperature (B2:B13) and heaters sold (D2:D13):
=CORREL(Beginning($B$2:$B$13, 0, ROWS($1:3)-ane), Starting time($B$ii:$B$13, 0, COLUMNS($A:A)-1))
In the first Kickoff office, ROWS($1:1) has transformed to ROWS($1:iii) because the 2d coordinate is relative, so information technology changes based on the relative position of the row where the formula is copied (two rows downwardly). Thus, ROWS() returns 3, from which nosotros subtract i, and go a range that is ii columns to the right of the source range, i.east. $D$two:$D$xiii (heater sales).
The second Beginning does not change the specified range $B$two:$B$13 (temperature) because COLUMNS($A:A)-one returns zero.
Every bit the upshot, our long formula turns into a uncomplicated CORREL($D$2:$D$13, $B$2:$B$13) and returns exactly the coefficient we want.
The formula in C18 that calculates a correlation coefficient for advertising cost (C2:C13) and sales (D2:D13) works in a similar manner:
=CORREL(OFFSET($B$2:$B$13, 0, ROWS($1:3)-one), OFFSET($B$ii:$B$13, 0, COLUMNS($A:B)-1))
The starting time OFFSET function is admittedly the same as depict above, returning the range of $D$two:$D$13 (heater sales).
In the second Get-go, COLUMNS($A:A)-1 changes to COLUMNS($A:B)-1 because we've copied the formula 1 column to the right. Consequently, First gets a range that is 1 column to the right of the source range, i.e. $C$2:$C$thirteen (advertising cost).
How to plot a correlation graph in Excel
When doing correlation in Excel, the best manner to get a visual representation of the relations between your data is to draw a scatter plot with a trendline. Here's how:
- Select two columns with numeric data, including column headers. The order of columns is important: the contained variable should be in the left column every bit this column is to exist plotted on the x axis; the dependent variable should exist in the correct column as information technology will be plotted on the y axis.
- On the Inset tab, in the Chats group, click the Scatter chart icon. This will immediately insert an XY besprinkle chart in your worksheet.
- Right click any data point in the chart and choose Add Trendline… from the context menu.
For the detailed stride-past-step instructions, please encounter:
- How to create scatter plot in Excel
- How to add together trendline to Excel chart
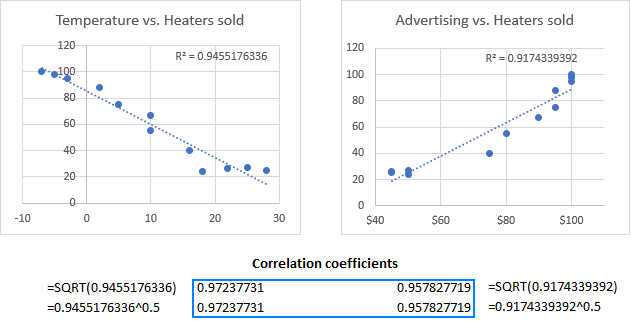
For our sample information set, the correlation graphs look like shown in the epitome below. Additionally, we displayed R-squared value, likewise chosen the Coefficient of Decision. This value indicates how well the trendline corresponds to the data - the closer R2 to i, the better the fit.
From the R2 value displayed on your scatterplot, you tin easily calculate the correlation coefficient:
- For better accuracy, get Excel to evidence more digits in the R-squared value than it does by default.
- Click the Rtwo value on the nautical chart, select information technology using the mouse, and press Ctrl + C to re-create information technology.
- Go a foursquare root of Rtwo either past using the SQRT function or by raising the copied R2 value to the power of 0.5.
For example, the Rtwo value in the second graph is 0.9174339392. So, you can find the correlation coefficient for Advertising and Heaters sold with one of these formulas:
=SQRT(0.9174339392)
=0.9174339392^0.five
As you can make certain, the coefficients calculated in this mode are perfectly in line with the correlation coefficients found in the previous examples, except the sign:
Potential problems with correlation in Excel
The Pearson Product Moment Correlation only reveals a linear relationship betwixt the ii variables. Pregnant, your variables may be strongly related in another, curvilinear, manner and still have the correlation coefficient equal to or close to zero.
The Pearson correlation is non able to distinguish dependent and independent variables. For example, when using the CORREL office to find the association between an average monthly temperature and the number of heaters sold, nosotros got a coefficient of -0.97, which indicates a loftier negative correlation. However, you could switch effectually the variables and go the same result. So, someone may conclude that higher heater sales crusade temperature to autumn, which obviously makes no sense. Therefore, when running correlation assay in Excel, be aware of the data yous are supplying.
Besides, the Pearson correlation is very sensitive to outliers. If you have one or more information points that differ greatly from the rest of the information, y'all may get a distorted picture of the relationship between the variables. In this case, you'd be wise to use the Spearman rank correlation instead.
That'southward how to do correlation in Excel. To have a closer wait at the examples discussed in this tutorial, you are welcome to download our sample workbook to Calculate Correlation in Excel. I thank you for reading and hope to see y'all on our weblog adjacent week!
Y'all may also exist interested in
Source: https://www.ablebits.com/office-addins-blog/2019/01/23/correlation-excel-coefficient-matrix-graph/
Posted by: pittmanheinink1945.blogspot.com

0 Response to "how to find hill coefficient from graph"
Post a Comment